[ 2주차 - 배울 내용 ]
- 논리 회귀 : 입력값과 범주 사이의 관계를 구하는 것
데이터로부터 타이타닉 생존자를 예측, 당뇨병 판단 등을 코드 수행을 통해 확인.
선형 회귀로 풀수 없는 문제을 논리회귀로 푸는 과정과 결과를 통해 case별 방법 확인.
- 전처리 (Pre-processing) : 오기입된 데이터, 다양한 단위 값과 분포 값을 정제 작업을 통해 학습에 필요한 정형화된 데이터로 만들기 위한 작업
전처리 기법들을 배우고, 전처리를 수행해야 하는 이유를 실습을 통해 익혀서 적용 해봄.
실업무에서는 7, 80% 정도의 업무를 차지하는 경우가 많음. 정확도에 많은 영향을 줌.
raw data를 가공해서 학습을 원활히 할 수 있도록 하는 과정.
- Classcification(분류)를 logistic regression(논리회귀)를 통해 배워 봄.
[ Logistic Regression(논리 회귀) ]
- 선형 회귀로 풀기 힘든 문제 예시.
대학교 시험 전 날 공부한 시간을 가지고 해당 과목의 이수 여부(Pass or fail)를 예측하는 문제
이문제의 입력값(공부한 시간), 출력값(이수여부, pass=1, fail=0) 이런 경우 이진 논리 회귀(Binary logistic regression)으로 해결 가능함.
Threshold(임계값)을 어떻게 주는냐에 따라 결과값(0 또는 1)에 대한 분포도가 달라짐.

동일 문제를 선형회귀로 풀려고 한다면, 아래와 같은 이상한 그림이 그려지며, 실제 얻으려고 하는 결과값(pass or fail)을 얻는게 어려워짐.
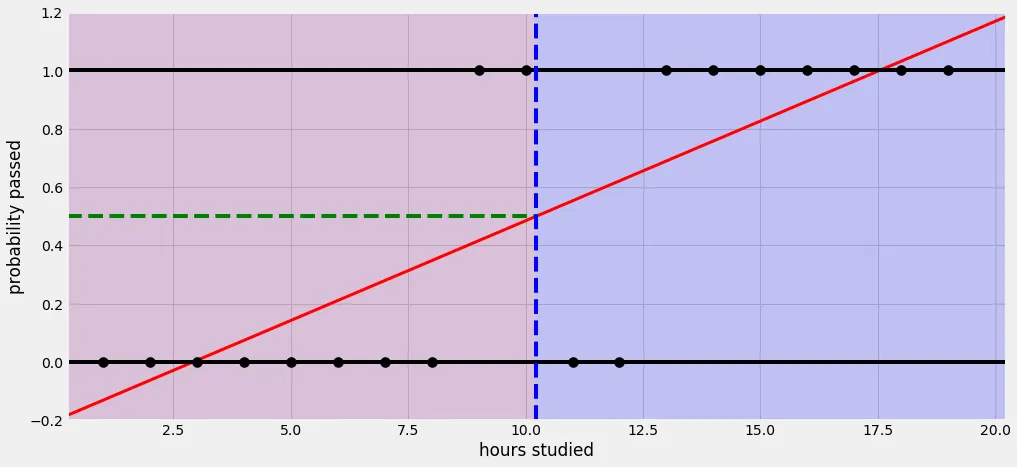
실 자연, 사회 현상에서는 특정 변수에 대한 확률값이 선형이 아닌 S 커브 형태를 따르는 경우가 많다고 함.
이렇게 S 커브를 함수로 표현한 것이 로지스틱 함수(Logistic function)이며, 딥러닝에서는 시그모이드 함수(Sigmoid function)라고 불림.
[ Logistic Regression - 가설과 손실함수 ]
- Sigmoid function
논리 회귀는 일반적인 계산은 선형회귀와 똑같지만, 축력에 시그모이드 함수를 붙여 0에서 1의 값에 귀결되도록 함.
아래와 같은 수식을 가지고 있음.

x(입력)값이 음수 방향으로 갈수록 y(출력)값은 0에 가까워지고,
x(입력)값이 양수 방향으로 갈수록 y(출력)값은 1에 가까워진다.
즉, 시그모이드 함수를 통과하면 0에서 1 사이의 값이 나온다.
- Sigmoid function의 가설
선형 회귀의 가설은 H(x) = Wx + b 였으며, 논리 회귀에서는 시그모이드 함수에 선형 회귀식을 x값을 대체하면 됨.


- Sigmoid function의 손실함수
정답 라벨(y)가 0이어야 하는 경우, 에측한 라벨이 0일 경우 확률이 1(=100%)이 되도록 해야 함.
반대로 예측한 라벨이 1일 경우 확률이 0(0%)이 되도록 만들어야 함.
이와는 반대로 정답 라벨 y가 1일 경우, 예측한 라벨이 1일때 확률이 1(=100%)이 되도록 만들어야 함.



위와 같이 가로축을 라벨(클래스)로 표시, 세로축을 확률로 표시한 그래프를 확률 분포 그래프라고 함.
확률 분포 그래프의 차이를 비교할 때에는 Crossentropy라는 함수를 사용.
그래프로 개념을 이해하면, 임의의 입력값에 대한 우리가 원하는 확률 분포 그래프를 만들도록 학습시키는 손실 함수임.
아래는 그 예시.

Keras에서는 이진 논리 회귀의 경우 binary_crossentropy 손실 함수를 사용.
[ Multinomial Logistic Regression(다항(중) 논리 회귀) ]
- 다항 논리 회귀와 One-hot encoding
단일 선택값(0 또는 1)을 가지는 논리 회귀에서 결과 값이 여러개로 나올 수 있는 다항 논리 회귀에서는 결과 값이 하나의 값이 아닌 여러가지 값을 가질 수 있는데. 이때 classcification 을 할 수 있도록 하는 방법 중. 한가지 방법으로 One-hot encoding 방법을 사용할 수 있음.
첫번째 예측 문제였던 대학교 시험 전날 공부한 시간에 따른 해당 과목의 pass 유,무(pass or fail)가 아닌, 해당 과목의 학점을 class로 나누는 것을 예측하는것(A, B, C, D, E, F 학점과 같은)

이때 컴퓨터가 해당 값들을 풀어서 처리하기 위해 취할 수 있는 출력값 그룹 형태를 표현하는게 One-hot encoding 이라고 보면 됨.
아래의 표를 참고.

One-hot encoding을 만드는 방법은 아래와 같다.(위 표 예시 참고)
- Class(라벨)의 개수만큼 배열 생성 후 그 요소 값들을 0으로 채운다.
- 각 class의 인덱스 위치를 정한다.
- 각 class에 해당하는 인덱스에 1을 넣는다.
- Softmax 함수와 손실함수
Softmax 함수는 선형 모델에서 나온 결과(Logit)를 모두 더하면 1이 되도록 만들어주는 함수.
모두 더해서 1이 되도록 만드는 이유는 예측의 결과를 확률(=Confidence)로 표현하기 위함.
우리가 One-hot encoding을 할 때, 라벨 값을 전부 더하면 1(=100%)이 되기 때문.


다항 논리 회귀에서 Softmax 함수를 통과 시킨 결과 값의 확률 분포 그래프를 그려서 만들어진 그래프의 모양에서, 단항 논리 회귀에서와 마찬가지로 가로축은 클래스(라벨)이 되고 세로축은 확률이 됨.
동일한 관점에서 확률 분포의 차이를 계산할 때에는 Crossentropy 함수를 사용. 항이 여러개가 되었다고 해서 이진 논리 회귀와의 차이는 없음.
기본적으로 데이터셋의 정답 라벨과 예측한 라벨의 확률 분포 그래프를 구해서 Crossentropy로 두 분포의 차이를 구하고, 그 차이를 최소화 하는 방향으로 학습을 시켜나가면 그것이 모델이 됨.

Keras에서는 다항 논리 회귀의 경우 categorical_crossentropy 손실 함수를 사용함.
[ 다양한 머신러닝 모델 ]
- Support vector machine (SVM)
다양한 분류 문제를 풀기 위해 활용되는 모델, SVM을 활용한 다양한 분류기(Classifier)가 있으며, 기본적인 개념은 아래와 같다.
예제로 고양이와 개를 분류하는 예를 들어 보면,


선이 해당 모델의 기준이 되는 모델식이 될 텐데. 어떻게 하면 가장 잘 구분이 될 수 있도록 그려야 하는지가 핵심.
이때, 고양이와 개와 직선간의 거리가 가장 최대가 될 수 있도록 그리면 가장 잘 구분이 된 것으로 말할 수 있음.
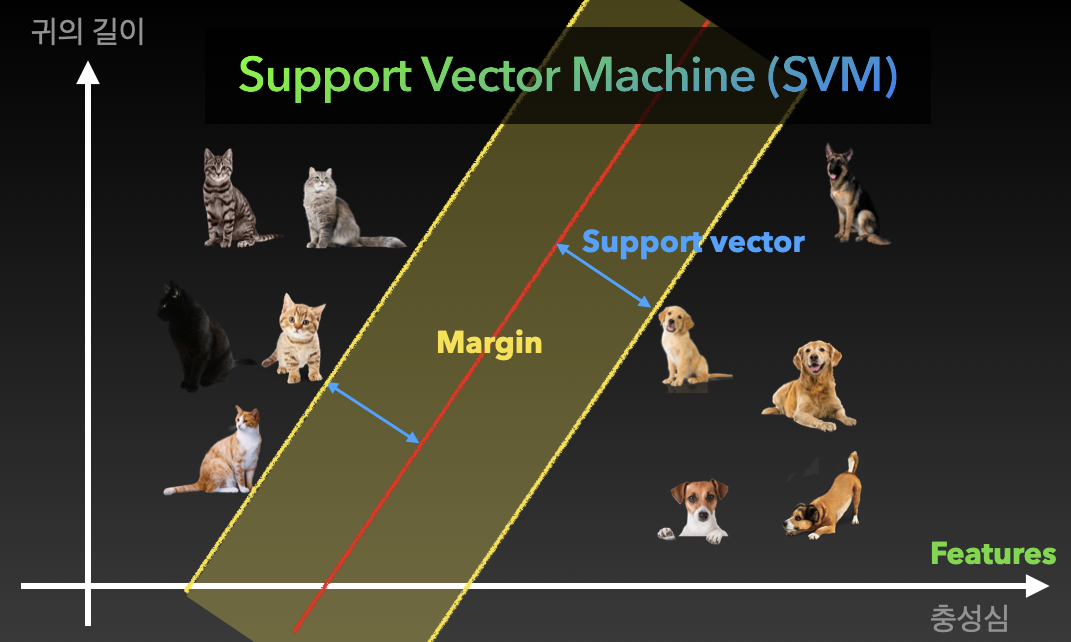
다만, 특정 요소의 분류를 위한 식으로 2가지 특성을 이용했을때 구분이 모호해 지거나, 부적합한 답이 도출 될 경우, 특성(Feature)을 추가하여 모델의 분류 기준을 높이는 방법을 사용.
상업적 모델의 경우 수십, 수백, 수만이상의 특성을 만들어서 분류의 기준으로 잡기도 함.
- 기타 머신러닝 모델 간단 소개
k-Nearest neighbors (KNN)
비슷한 특성을 가진 개체끼리 군집화하는 알고리즘.
아래와 같이 하얀 고양이가 새로 나타났을때 일정 거리내에 다른 개체들의 개수(k)를 보고 새로 들어온 개체의 위치를 결정하게 하는 알고리즘.

Decision tree (의사결정 나무)
스무고개식의 의사결정을 통한 분류 알고리즘으로 , 특성에 대한 Yes or No를 반복적으로 거쳐서 해당 요소를 특성 짓도록 하는 방식으로 성능이 좋아서 간단한 문제를 빠르게 풀때 자주 사용함.


Random forest (Decision tree 강화 버전)
의사결정나무 알고리즘을 여러개 합친 모델이며, 의사결정나무는 한 사람이 결정하는 방식이라면 랜덤 포레스터는 여러 의사결정 체계의 합으로 투표하여 결정 짓는 방식의 알고리즘.

[ 머신러닝에서의 전처리(Preprocessing) ]
- 전처리(Preprocessing)란?
넓은 의미에서 데이터 정제작업을 뜻함.
- 필요없는 데이터를 찾아서 지우고, 필요한 데이터만을 취하는것
- null 값이 있는 행은 삭제하는 것,
- 정규화(Normalization) 또는 표준화(Standardization) 과정 등이 포함.
- 전체 ML 실무에서 약 70~80 %를 차지할 정도로 많은 작업을 수행하며, 매우 중요한 단계임.
- 전처리(Preprocessing) - 정규화와 표준화가 필요한 이유 예시

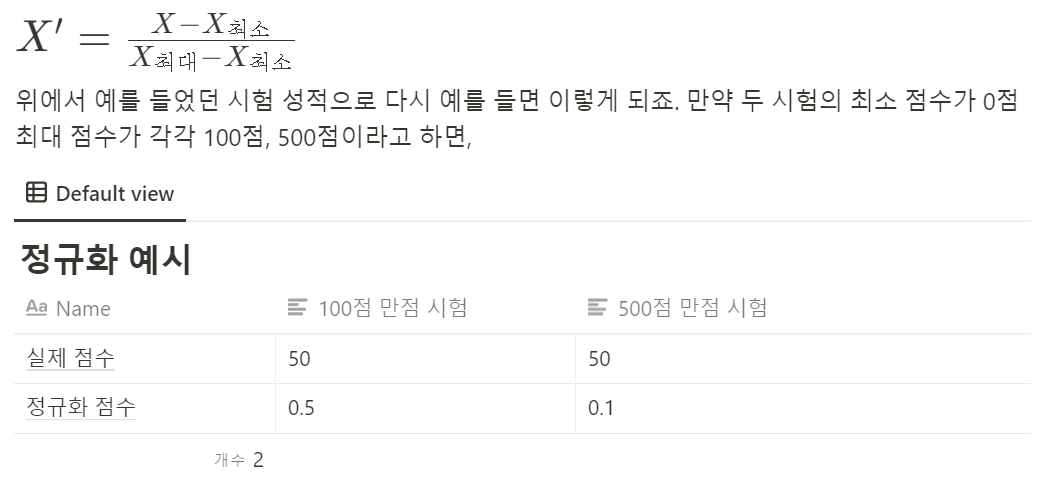
- 정규화 (Normalization)
정규화는 데이터를 0과 1사이의 범위를 가지도록 만듬.
같은 특성값을 가진데이터 중에서 가장 작은 값을 0으로 만들고, 가장 큰 값을 1로 만드는 방법.
결과적으로 다양한 특성의 값들을 0에서 1사이의 값을 가지도록 만들어서 특정 분류 및 가치 평가에 사용되는 다양한 수식과 데이터 조정에서도 일관된 평가 값이 나타날 수 있도록 함.
- 표준화 (Standardization)
표준화는 데이터의 분포를 정규분포로 바꿔줌. 데이터의 평균이 0이 되도록 하고, 표준편차가 1이 되도록 만들어줌. 수식은 아래와 같음.

데이터의 평균을 0으로 만들어주면 데이터의 중심이 0에 맞춰지게(Zero-centered) 됨. 표준편차를 1로 만들어주면 데이터가 정규화(Normalizaed)되며, 표준화 과정을 거친 데이터를 가지고 모델링을 하게 되면, 학습 속도(최저점 수렴 속도)가 빠르게 되고, Local minima에 빠질 가능성이 줄어듬.

정규화의 표준화를 나타내는 그래프의 변화

[ 이진 논리 회귀(Binary Logistic Regression) 실습 ]
- 타이타닉 생존자 예측하기
캐글(kaggle) 사이트에서 가장 유명한 데이터인 타이타닉 승객 정보를 이용하여 이진 논리회귀를 실습.
완료 코드 스니펫 : https://colab.research.google.com/drive/1ElLU8rpS1vcbq3U75dcyQJe7GHNad8Bb?usp=sharing
(자신의 데이터 공간으로 복제해서 사용할것)
2주차 실습 - 01. 이진 논리 회귀
Colaboratory notebook
colab.research.google.com
진행 과정
- 데이터 다운 받기
- 필요한 패키지 임포트하기
- 데이터 로딩하기
- 전처리하기
- 모델 학습시키기
- 데이터 다운 받기
기존 kaggle 계정 정보를 이용해서 나의 colab 작업 공간으로 데이터를 다운로드 한 뒤 압축을 해제하여 데이터 사용 준비를 함.
import os
os.environ['KAGGLE_USERNAME'] = 'username' # username
os.environ['KAGGLE_KEY'] = 'key' # keyconsole command 처리로 데이터 셋 다운로드 및 압축해제 실행
!kaggle datasets download -d heptapod/titanic
!unzip titanic.zip
- 필요한 패키지 임포트하기
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam, SGD
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
- 데이터 로딩하기
df = pd.read_csv('train_and_test2.csv')
- 전처리 하기
1) 사용할 컬럼 추출하기
df = pd.read_csv('train_and_test2.csv', usecols=[
'Age', # 나이
'Fare', # 승차 요금
'Sex', # 성별
'sibsp', # 타이타닉에 탑승한 형제자매, 배우자의 수
'Parch', # 타이타니게 탑승한 부모, 자식의 수
'Pclass', # 티켓 등급 (1, 2, 3등석)
'Embarked', # 탑승국
'2urvived' # 생존 여부 (0: 사망, 1: 생존)
])
* 입력된 데이터 셋 미리보기


2) 비어있는 행 없애기 (숫자값이 없거나, 문자로 되어 있거나 등등)
print(df.isnull().sum()) # 비어있는 값(null 또는 na)이 있는지 확인
print(len(df)) # 현재의 데이터셋의 크기값 확인
df = df.dropna() # 비어있는 값을 포함한 행을 제거
print(len(df)) # 제거 후 데이터셋의 크기값 확인
3) X, Y 데이터 분할하기
본격적인 데이터 모델링을 위한 x,y 데이터 분할하기, 생존 상태를 찾아내기 위한 모델링
x_data = df.drop(columns=['2urvived'], axis=1) # 생존 여부 컬럼만 drop
x_data = x_data.astype(np.float32) # @keras는 float32, 소숫점 처리만 가능하기에 데이터 형식을 변경
x_data.head(5) # 변경된 x_data의 앞에서 5번째값 까지를 확인, 변경이 제대로 된 것인지를 검증
y_data = df[['2urvived']] # y축 데이터는 생존여부만 판단하면 되기에
y_data = y_data.astype(np.float32)
y_data.head(5) # 변경된 y_data의 앞에서 5번째값 까지를 확인, 변경이 제대로 된 것인지를 검증

4) 표준화 하기
https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html
평균을 0으로 맞추고, 표준편차를 1로 맞추는 방법, 자세한 내용은 해당 페이지를 참고.
sklearn.preprocessing.StandardScaler
Examples using sklearn.preprocessing.StandardScaler: Release Highlights for scikit-learn 1.0 Release Highlights for scikit-learn 1.0, Release Highlights for scikit-learn 0.23 Release Highlights for...
scikit-learn.org
z = (x - u) / s
z = (x - 평균) / 표준편차
scaler = StandardScaler() # scikit-learn의 StandardScaler를 호출
x_data_scaled = scaler.fit_transform(x_data) @ 표준화 과정이 필요한 x_data 영역만 표준화 처리
print(x_data.values[0]) # 표준화 과정 이전의 원래 데이터셋의 값들
print(x_data_scaled[0]) # 표준화 과정 처리 후 데이터셋의 값들
[22. 7.25 0. 1. 0. 3. 2. ]
[-0.58026063 -0.5018386 -0.74189967 0.48027173 -0.44540733 0.8404475
0.6229398 ]
5) 학습/검증 데이터 분할하기
x_train, x_val, y_train, y_val = train_test_split(x_data, y_data, test_size=0.2, random_state=2021)
print(x_train.shape, x_val.shape)
print(y_train.shape, y_val.shape)
(1045, 7) (262, 7)
(1045, 1) (262, 1)
- 모델 학습시키기
model = Sequential([
Dense(1, activation='sigmoid')
])
model.compile(loss='binary_crossentropy', optimizer=Adam(lr=0.01), metrics=['acc'])
# 모델을 만든다., 손실알고리즘은 crossentropy를 사용하는데 keras는 binary_crossentropy를 사용,
# optimizer는 Adam(lr=learning rate 0.01)을 사용, 처음으로 metrics라는 인수가 나오는데
# 이는 손실함수 만으로는 정확한 학습 결과를 도출하기 어려워서 특히, 분류(classcification) 문제를 풀때에는
# acc라는 metric을 잘 씀.
# 만들어진 모델에 해당 데이터를 적용해가며 , 학습시킨다.
model.fit(
x_train,
y_train,
validation_data=(x_val, y_val), # 검증 데이터를 넣어주면 한 epoch이 끝날때마다 자동으로 검증
epochs=20 # epochs 복수형으로 쓰기!
)
/usr/local/lib/python3.7/dist-packages/keras/optimizer_v2/adam.py:105: UserWarning: The `lr` argument is deprecated, use `learning_rate` instead.
super(Adam, self).__init__(name, **kwargs)
Epoch 1/20
33/33 [==============================] - 1s 8ms/step - loss: nan - acc: 0.6781 - val_loss: nan - val_acc: 0.7557
Epoch 2/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 3/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 4/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 5/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 6/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 7/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 8/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 9/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 10/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 11/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 12/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 13/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 14/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 15/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 16/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 17/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 18/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 19/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
Epoch 20/20
33/33 [==============================] - 0s 3ms/step - loss: nan - acc: 0.7345 - val_loss: nan - val_acc: 0.7557
<keras.callbacks.History at 0x7f06c2838490>
[ 다항 논리 회귀(Multinomial Logistic Regression) 실습 ]
- 와인 분류 예제
와인의 도수, 산도, 색 등을 이용해서 3개의 클래스로 분류해 보는 실습.
완료 코드 스니펫 : https://colab.research.google.com/drive/1FuzzhcnIOzUcZQ7soSfq0IOxZw5Uos5z?usp=sharing
(자신의 데이터 공간으로 복제해서 사용할것)
2주차 실습 - 02. 다항 논리 회귀
Colaboratory notebook
colab.research.google.com
진행 과정
- 데이터 다운 받기
- 필요한 패키지 임포트하기
- 데이터 로딩하기
- 전처리하기
- 모델 학습시키기
- 처리 코드 및 명령
# kaggle 데이터셋 다운로드를 위한 사전 계정 정보와 생성되어 있던 key값을 입력
import os
os.environ['KAGGLE_USERNAME'] = 'username' # username
os.environ['KAGGLE_KEY'] = 'kaggle key' # key
# kaggle 데이터셋 다운로드
!kaggle datasets download -d brynja/wineuci
Downloading wineuci.zip to /content
0% 0.00/4.20k [00:00<?, ?B/s]
100% 4.20k/4.20k [00:00<00:00, 8.26MB/s]
# 압축 해제
!unzip wineuci.zip
Archive: wineuci.zip
inflating: Wine.csv
# keras 및 필요한 python package 로딩
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam, SGD
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import OneHotEncoder
# 데이터셋 로드
df = pd.read_csv('Wine.csv')
# 불러온 데이터셋 확인
df.head(5)
# 실행 결과
1 14.23 1.71 2.43 15.6 127 2.8 3.06 .28 2.29 5.64 1.04 3.92 1065
0 1 13.20 1.78 2.14 11.2 100 2.65 2.76 0.26 1.28 4.38 1.05 3.40 1050
1 1 13.16 2.36 2.67 18.6 101 2.80 3.24 0.30 2.81 5.68 1.03 3.17 1185
2 1 14.37 1.95 2.50 16.8 113 3.85 3.49 0.24 2.18 7.80 0.86 3.45 1480
3 1 13.24 2.59 2.87 21.0 118 2.80 2.69 0.39 1.82 4.32 1.04 2.93 735
4 1 14.20 1.76 2.45 15.2 112 3.27 3.39 0.34 1.97 6.75 1.05 2.85 1450
# 해당 데이터프레임에는 헤더가 없어서 헤더를 채워주면 됨.
df = pd.read_csv('Wine.csv', names=[
'name'
,'alcohol'
,'malicAcid'
,'ash'
,'ashalcalinity'
,'magnesium'
,'totalPhenols'
,'flavanoids'
,'nonFlavanoidPhenols'
,'proanthocyanins'
,'colorIntensity'
,'hue'
,'od280_od315'
,'proline'
])
# 채워진 헤더 값을 포함한 데이터셋 출력
df.head(5)
# 실행결과
name alcohol malicAcid ash ashalcalinity magnesium totalPhenols flavanoids nonFlavanoidPhenols proanthocyanins colorIntensity hue od280_od315 proline
0 1 14.23 1.71 2.43 15.6 127 2.80 3.06 0.28 2.29 5.64 1.04 3.92 1065
1 1 13.20 1.78 2.14 11.2 100 2.65 2.76 0.26 1.28 4.38 1.05 3.40 1050
2 1 13.16 2.36 2.67 18.6 101 2.80 3.24 0.30 2.81 5.68 1.03 3.17 1185
3 1 14.37 1.95 2.50 16.8 113 3.85 3.49 0.24 2.18 7.80 0.86 3.45 1480
4 1 13.24 2.59 2.87 21.0 118 2.80 2.69 0.39 1.82 4.32 1.04 2.93 735
# 정답 라벨의 개수 확인
sns.countplot(x=df['name'])
<matplotlib.axes._subplots.AxesSubplot at 0x7fb303ce26d8>
# 전처리
# 비어있는 행 확인
print(df.isnull().sum())
# 실행 결과
name 0
alcohol 0
malicAcid 0
ash 0
ashalcalinity 0
magnesium 0
totalPhenols 0
flavanoids 0
nonFlavanoidPhenols 0
proanthocyanins 0
colorIntensity 0
hue 0
od280_od315 0
proline 0
dtype: int64
# x,y 데이터 분할
# x 데이터 입력
x_data = df.drop(columns=['name'], axis=1)
x_data = x_data.astype(np.float32)
x_data.head(5)
# 실행 결과
alcohol malicAcid ash ashalcalinity magnesium totalPhenols flavanoids nonFlavanoidPhenols proanthocyanins colorIntensity hue od280_od315 proline
0 14.23 1.71 2.43 15.600000 127.0 2.80 3.06 0.28 2.29 5.64 1.04 3.92 1065.0
1 13.20 1.78 2.14 11.200000 100.0 2.65 2.76 0.26 1.28 4.38 1.05 3.40 1050.0
2 13.16 2.36 2.67 18.600000 101.0 2.80 3.24 0.30 2.81 5.68 1.03 3.17 1185.0
3 14.37 1.95 2.50 16.799999 113.0 3.85 3.49 0.24 2.18 7.80 0.86 3.45 1480.0
4 13.24 2.59 2.87 21.000000 118.0 2.80 2.69 0.39 1.82 4.32 1.04 2.93 735.0
# y 데이터 입력
y_data = df[['name']]
y_data = y_data.astype(np.float32)
y_data.head(5)
# 실행 결과
name
0 1.0
1 1.0
2 1.0
3 1.0
4 1.0
# 데이터 표준화
scaler = StandardScaler()
x_data_scaled = scaler.fit_transform(x_data)
print(x_data.values[0])
print(x_data_scaled[0])
# 표준화 실행 결과
[1.423e+01 1.710e+00 2.430e+00 1.560e+01 1.270e+02 2.800e+00 3.060e+00
2.800e-01 2.290e+00 5.640e+00 1.040e+00 3.920e+00 1.065e+03]
[ 1.5186119 -0.5622497 0.2320528 -1.1695931 1.9139051 0.8089973
1.0348189 -0.65956306 1.2248839 0.2517168 0.3621771 1.8479197
1.013009 ]
# One-hot encoding
encoder = OneHotEncoder()
y_data_encoded = encoder.fit_transform(y_data).toarray()
print(y_data.values[0])
print(y_data_encoded[0])
# 출력 결과
[1.]
[1. 0. 0.]
# 학습 / 검증 데이터 분할
x_train, x_val, y_train, y_val = train_test_split(x_data_scaled, y_data_encoded, test_size=0.2, random_state=2021)
print(x_train.shape, x_val.shape)
print(y_train.shape, y_val.shape)
(142, 13) (36, 13)
(142, 3) (36, 3)
# 모델 학습
model = Sequential([
Dense(3, activation='softmax')
])
model.compile(loss='categorical_crossentropy', optimizer=Adam(lr=0.02), metrics=['acc'])
model.fit(
x_train,
y_train,
validation_data=(x_val, y_val), # 검증 데이터를 넣어주면 한 epoch이 끝날때마다 자동으로 검증
epochs=20 # epochs 복수형으로 쓰기!
)
# 학습 실행 결과
Epoch 1/20
5/5 [==============================] - 1s 115ms/step - loss: 1.2892 - acc: 0.3798 - val_loss: 1.0719 - val_acc: 0.4444
Epoch 2/20
5/5 [==============================] - 0s 11ms/step - loss: 0.6915 - acc: 0.7560 - val_loss: 0.6363 - val_acc: 0.7222
Epoch 3/20
5/5 [==============================] - 0s 11ms/step - loss: 0.4333 - acc: 0.8604 - val_loss: 0.4207 - val_acc: 0.8333
Epoch 4/20
5/5 [==============================] - 0s 12ms/step - loss: 0.2794 - acc: 0.9227 - val_loss: 0.3199 - val_acc: 0.8889
Epoch 5/20
5/5 [==============================] - 0s 12ms/step - loss: 0.1802 - acc: 0.9590 - val_loss: 0.2684 - val_acc: 0.8611
Epoch 6/20
5/5 [==============================] - 0s 11ms/step - loss: 0.1637 - acc: 0.9548 - val_loss: 0.2342 - val_acc: 0.8889
Epoch 7/20
5/5 [==============================] - 0s 12ms/step - loss: 0.1260 - acc: 0.9840 - val_loss: 0.2099 - val_acc: 0.8889
Epoch 8/20
5/5 [==============================] - 0s 12ms/step - loss: 0.1150 - acc: 0.9788 - val_loss: 0.1912 - val_acc: 0.8889
Epoch 9/20
5/5 [==============================] - 0s 13ms/step - loss: 0.0923 - acc: 0.9910 - val_loss: 0.1774 - val_acc: 0.8889
Epoch 10/20
5/5 [==============================] - 0s 11ms/step - loss: 0.0884 - acc: 0.9814 - val_loss: 0.1647 - val_acc: 0.8889
Epoch 11/20
5/5 [==============================] - 0s 12ms/step - loss: 0.0819 - acc: 0.9832 - val_loss: 0.1561 - val_acc: 0.8889
Epoch 12/20
5/5 [==============================] - 0s 13ms/step - loss: 0.0750 - acc: 0.9832 - val_loss: 0.1503 - val_acc: 0.8889
Epoch 13/20
5/5 [==============================] - 0s 11ms/step - loss: 0.0635 - acc: 1.0000 - val_loss: 0.1451 - val_acc: 0.9167
Epoch 14/20
5/5 [==============================] - 0s 49ms/step - loss: 0.0546 - acc: 1.0000 - val_loss: 0.1392 - val_acc: 0.9167
Epoch 15/20
5/5 [==============================] - 0s 12ms/step - loss: 0.0633 - acc: 1.0000 - val_loss: 0.1360 - val_acc: 0.9167
Epoch 16/20
5/5 [==============================] - 0s 12ms/step - loss: 0.0528 - acc: 1.0000 - val_loss: 0.1339 - val_acc: 0.9167
Epoch 17/20
5/5 [==============================] - 0s 11ms/step - loss: 0.0544 - acc: 1.0000 - val_loss: 0.1329 - val_acc: 0.9167
Epoch 18/20
5/5 [==============================] - 0s 11ms/step - loss: 0.0447 - acc: 1.0000 - val_loss: 0.1313 - val_acc: 0.9167
Epoch 19/20
5/5 [==============================] - 0s 12ms/step - loss: 0.0470 - acc: 1.0000 - val_loss: 0.1291 - val_acc: 0.9167
Epoch 20/20
5/5 [==============================] - 0s 12ms/step - loss: 0.0406 - acc: 1.0000 - val_loss: 0.1284 - val_acc: 0.9167
<tensorflow.python.keras.callbacks.History at 0x7fb2ff6e5630>
[ ]
[ 다항 논리 회귀(Multinomial Logistic Regression) 실습 - 숙제(당뇨병 진단) ]
- 연령, 혈압, 인슐린 수치 등으로 당뇨병 진단 모델 개발
https://colab.research.google.com/drive/1c58INL86jHX0Yfj58Kj7wKsfz-DHEBqV?usp=sharing
2주차 실습 과제 - 당뇨병 진단
Colaboratory notebook
colab.research.google.com
'ICT 학습' 카테고리의 다른 글
| 웹개발 종합반 - 2주차 (0) | 2022.04.25 |
|---|---|
| 이미지 처리로 시작하는 딥러닝 - 2주차 (0) | 2022.04.24 |
| 웹개발 종합반 - 1주차 (0) | 2022.04.17 |
| 이미지 처리로 시작하는 딥러닝 - 1주차 (0) | 2022.04.16 |
| 머신러닝 기본부터 다시 배우기 - 1주차 (0) | 2022.04.16 |



