[ 3주차 - 배울 내용 ]
- 딥러닝의 역사를 가볍게 배워본다.
- 신경망을 만드는 데 필요한 각종 개념을 알아본다.
- 신경망을 직접 디자인 해 본다.
[ 3주차 - 배울 내용 ]
- 딥러닝(Deep Learning) 이란?
탄생 배경과 주요 개념들을 배워봄. 딥러닝은 머신러닝의 한 분야

우리가 지금까지 배운 선형회귀와 논리회귀는 모두 1차 함수를 이용해서 문제를 풀었는데, 자연계에는 직선으로 설명할 수 없는 문제들이 훨씬 많음.
이런 복잡한 문제들을 풀기 위해 선형회귀를 여러번 반복해봄

하지만 선형회귀를 여러번 반복한다고해서 비선형(선형이 아닌 것)이 되는 것은 아니었음.
y = W_2(W_1x +b_1) + b_2 = (W_1 W_2)x+(W_1b_1+b_2)

그래서 선형회귀 사이에 비선형의 무엇인가를 넣어야 한다고 생각했고,

이와같이 층(Layer)을 여러개 쌓기 시작했고 이렇게 만들어진 모델은 잘 동작함. 층을 깊게(Deep) 쌓는다고 해서 딥러닝이라고 불리게 됨!
딥러닝의 다른 단어 표현
1. 딥러닝(Deep learning)
2. Deep neural networks
3. Multilayer Perceptron(MLP)
- 딥러닝(Deep Learning)의 주요 개념과 기법.
신경망을 실제로 구성하는데 필요한 다양한 개념과 기법들을 알아봄.
- 배치 사이즈와 에폭
- 활성화 함수
- 과적합과 과소적합
- 데이터 증강
- 드랍아웃
- 앙상블
- 학습률 조정
[ 딥러닝의 역사 ]
- XOR 문제
기존의 머신러닝은 AND, OR 문제로부터 시작.

위와 같은 문제를 풀기위해서는 직선 하나만 있으면 되는데 그 직선은 논리회귀로 쉽게 만들 수 있었음.

이 수식을 아래와 같이 그림으로 나타낼 수 있으며. 이런 모양을 Perceptron(퍼셉트론)이라고 불렀음.

w0, w1, w2 의 값만 잘 지정해주면 우리가 원하는 출력을 계산할 수 있었기 때문에 사람들은 흥분하기 시작했고.
AND, OR 문제를 잘 조합하면 생각하는 기계를 만들 수 있겠다!라고 전 인류가? 흥분의 도가니에 빠지게 됨.
실제로 1958년 뉴욕타임즈에는 아래와 같은 기사가 실렸다고함.

논리 게이트를 조합하면 생각하는 기계를 만들 수 있겠다 - feat. The New York Times, Jul 08 1958
그런데 선형회귀로는 AND, OR 문제는 잘 풀었지만 XOR 문제는 풀지 못했음.

Perceptron을 여러개 붙인 Multilayer Perceptrons (MLP)라는 개념을 도입해서 문제를 풀어보려고 했음.

많은 사람들이 MLP로 XOR 문제를 풀기 위해 도전했지만 Marvin Minsky는 한 개의 perceptron으로는 XOR를 풀 수 없고,
MLP를 써야하는데 각각의 weight과 bias를 학습시키는 데 너무 많은 계산이 필요하므로 당시 기술로는 불가능하다고 주장했음.

그래서 많은 사람들이 이 문제를 포기하게 되고 딥러닝(=MLP, Neural networks)의 발전은 짧게는 10년, 길게는 20년 정도 후퇴하게 됨.
- Backpropagation (역전파)
계속되어온 딥러닝의 침체기는 1974년에 발표된 Paul Werbos(폴)이라는 사람의 박사 논문 덕분에 끝이 나게 됨.

- 우리는 W(weight)와 b(bias)를 이용해서 주어진 입력을 가지고 출력을 만들어 낼 수 있다.
- 그런데 MLP가 만들어낸 출력이 정답값과 다를 경우 W와 b를 조절해야한다.
- 그것을 조절하는 가장 좋은 방법은 출력에서 Error(오차)를 발견하여 뒤에서 앞으로 점차 조절하는 방법이 필요하다.
이 알고리즘은 관심받지 못하다가 1986년에 Hinton 교수가 똑같은 방법을 독자적으로 발표하면서 알려지게 되었음.
이렇게 해서 XOR 문제는 MLP를 풀 수 있게 되어 해결될 수 있었고 그 핵심방법은 바로 역전파 알고리즘의 발견이었음.

[ Deep Neural Networks 구성 방법 ]
- Layer(층) 쌓기
딥러닝에서 네트워크의 구조는 크게 3가지로 나누어짐.

Input layer(입력층): 네트워크의 입력 부분. 우리가 학습시키고 싶은 x 값.
Output layer(출력층): 네트워크의 출력 부분. 우리가 예측한 값, 즉 y 값.
Hidden layers(은닉층): 입력층과 출력층을 제외한 중간층.
풀어야하는 문제에 따라 입력층과 출력층의 모양은 정해져 있고, 따라서 우리가 신경써야할 부분은 은닉층임. 은닉층은 완전연결 계층 (Fully connected layer = Dense layer)으로 이루어져 있음.
기본적인 뉴럴 네트워크(Deep neural networks)에서는 보통 은닉층에 중간 부분을 넓게 만드는 경우가 많으며, 예를 들면 보편적으로 아래와 같이 노드의 개수가 점점 늘어나다가 줄어드는 방식으로 구성함.

곧 배우는 활성화 함수를 어디다가 넣어야하는지도 중요하며, 보편적인 경우 모든 은닉층 바로 뒤에 위치함.

- 네트워크의 Width(너비)와 Depth(깊이)
만약 우리가 수많은 시간을 투자하여 완성한 적당한 연산량을 가진, 적당한 정확도의 딥러닝 모델이 있다고 가정한다면,
그 모델은 Baseline model(베이스라인 모델)이라고 보편적으로 지칭함. 예를 들어 우리가 만든 베이스라인 모델의 크기는 다음과 같음.
- 입력층: 4
- 첫 번째 은닉층: 8
- 두 번째 은닉층: 4
- 출력층: 1
우리는 이 베이스라인 모델을 가지고 여러가지 실험(튜닝)을 해볼 수 있는데. 가장 간단하게 성능을 테스트할 수 있는 방법이 바로 모델의 너비와 깊이를 가지고 테스트하는 것임.
네트워크의 너비를 늘리는 방법
네트워크의 은닉층의 개수를 그대로 두고 은닉층의 노드 개수를 늘리는 방법. 예를 들어 너비를 베이스라인 모델의 2배로 늘리는 실험을 하겠다고 하면 네트워크는 아래와 같이 됨.

네트워크의 깊이를 늘리는 방법
네트워크의 은닉층의 개수를 늘리는 방법.

네트워크의 너비와 깊이를 모두 늘리는 방법
위의 두 가지의 방법을 모두 사용.

실무에서는 네트워크의 너비와 깊이를 바꾸면서 실험을 많이 함. 그만큼 시간도 많이 들고 지루한 작업임 ㅠㅠ.
다음 파트에서 배울 과적합과 과소적합을 피하기위해서는 꼭 필요한 노가다로 봄.
[ 딥러닝의 주요 개념 ]
- Batch size, Epoch (배치 사이즈, 에폭)
모델을 학습시키는 데 쓰이는 '단위'에 대해 알아보자.
batch와 iteration(배치와 이터레이션)
약 우리가 10,000,000개의 데이터셋을 가지고 있다고 가정하고, 10,000,000개의 데이터셋을 한꺼번에 메모리에 올리고 학습시키려면 엄청난 용량을 가진 메모리가 필요하고 그 메모리를 사는데 (메모리가 없다면 개발하는데) 천문학적인 비용이 들 것임.
따라서 우리는 이 데이터셋을 작은 단위로 쪼개서 학습을 시키는데 쪼개는 단위를 배치(Batch)라고 부르며, 예를 들어서 1,000만개의 데이터셋을 1,000개 씩으로 쪼개어 10,000번을 반복하는 것. 이 반복하는 과정을 Iteration(이터레이션)이라고 부름.
epoch(에폭)
보통 머신러닝에서는 똑같은 데이터셋을 가지고 반복 학습을 하게됨, 이 과정은 우리가 수능시험을 대비해서 모의고사 문제를 여러번 풀어보는 과정하고 비슷함. 만약 100번 반복 학습을 한다면 100 epochs(에폭)을 반복한다고 말함.
batch를 몇 개로 나눠놓았냐에 상관 없이 전체 데이터셋을 한 번 돌 때 한 epoch이 끝남.
따라서 1천만개의 데이터셋을 1천개 단위의 배치로 쪼개면, 1만개의 배치가 되고, 이 1만개의 배치를 100에폭을 돈다고 하면 1만 * 100 = 100만번의 이터레이션을 도는 것이 됨.!

- Activation functions (활성화 함수)
활성화 함수는 뇌의 뉴런이 다음 뉴런으로 전달할 때 보내는 전기신호의 특성에서 영감을 받아 만들어졌음.!
우리가 앞서 배운 MLP의 연결 구조를 여러개의 뉴런이 연결된 모습과 비슷하다고 가정하고 생각해보자.!

수많은 뉴런들은 서로 서로 빠짐없이 연결되어 있다. 그런데 뉴런들은 전기 신호의 크기가 특정 임계치(Threshold)를 넘어야만 다음 뉴런으로 신호를 전달하도록 설계되어 있음. 연구자들은 뉴런의 신호전달 체계를 흉내내는 함수를 수학적으로 만들었는데, 전기 신호의 임계치를 넘어야 다음 뉴런이 활성화 한다고해서 활성화 함수라고 부름.
활성화 함수는 비선형 함수여야 함. 위에서 딥러닝은 비선형 함수를 사용한다고 했었는데 비선형 함수의 대표적인 예가 바로 시그모이드 함수. 따라서 비선형 함수 자리에 시그모이드를 넣으면 이렇게 됨.

이런 비선형의 활성화 함수를 사용하여 다음 뉴런을 활성화 시킬지를 결정할 수 있음. 다시 한번 시그모이드 함수를 보면 아래와 같음.

시그모이드 함수는 x가 -6보다 작을 때는 0에 가까운 값을 출력으로 내보내서 비활성 상태를 만들며, 반대로 x가 6보다 클때는 1에 가까운 값을 출력으로 내보내서 활성 상태로 만듬.
이런 활성화 함수는 여러가지 종류가 있는데요. 그래프로 보면 아래와 같음.

딥러닝에서 가장 많이 보편적으로 쓰이는 활성화함수는 단연 ReLU(렐루) 임. 왜냐하면 다른 활성화 함수에 비해 학습이 빠르고, 연산 비용이 적고, 구현이 간단하기 때문.
대부분 딥러닝 모델을 설계할 때는 ReLU를 기본적으로 많이 쓰고, 여러 활성화 함수를 교체하는 노가다를 거쳐 최종적으로 정확도를 높이는 작업을 동반합니다. 이러한 노가다의 과정을 모델 튜닝이라고 부름.
- Overfitting, Underfitting (과적합, 과소적합)
딥러닝 모델을 설계/튜징하고 학습시키다 보면 가끔씩 Training loss는 점점 낮아지는데 Validation loss가 높아지는 시점이 있으며, 그래프로 표시하면 아래와 같은 현상임.

이런 현상을 과적합 현상이라고 함. 우리가 풀어야하는 문제의 난이도에 비해 모델의 복잡도(Complexity)가 클 경우 가장 많이 발생하는 현상. 시험에 빗대어 얘기하면 모의고사의 정답 번호를 달달외워서 모의고사는 100점을 받는데, 실제로 수능시험을 보면 틀리는 문제가 더 많아지는 현상과 비슷? ^^.
반대로 우리가 풀어야하는 문제의 난이도에 비해 모델의 복잡도가 낮을 경우 문제를 제대로 풀지 못하는 현상을 과소적합이라고 함.
따라서 우리는 적당한 복잡도를 가진 모델을 찾아야 하고 수십번의 튜닝 과정을 거쳐 최적합(Best fit)의 모델을 찾아야함.
딥러닝 모델을 학습시키다보면 보통 과소적합보다는 과적합때문에 골치를 썩는 경우가 많습니다. 과적합을 해결하는 방법에는 여러가지 방법이 있지만 대표적인 방법으로는 데이터를 더 모으기, Data augmenation, Dropout 등이 있음.
[ 딥러닝의 주요 스킬 ]
- Data augmentation (데이터 증강기법)
과적합을 해결할 가장 좋은 방법은 데이터의 개수를 늘리는 방법임. 하지만 실무에서는 데이터가 넘쳐나기는 커녕 부족한 경우가 매우 많음. 부족한 데이터를 보충하기위해 우리는 데이터 증강기법이라는 꼼수아닌 꼼수를 사용함. 데이터 증강기법은 이미지 처리 분야의 딥러닝에서 주로 사용하는 기법임. 데이터 증강기법은 아래 한 장의 이미지로 설명이 가능함.

원본 이미지 한 장을 여러가지 방법으로 복사를 함. 사람의 눈으로 보았을 때 위의 어떤 사진을 보아도 사자인 것처럼 딥러닝 모델도 똑같이 보도록 학습시킴. 이 방법을 통해 더욱 강건한 딥러닝 모델을 만들 수 있음.
데이터 증강기법은 반드시 정해진 방법들을 사용해야 하는 것이 아님. 데이터가 부족할 때 이미 있는 데이터 사용하여 증강시키는 개념으로 여러분들의 방법을 사용해서 증강 방법을 새로 만들어 낼 수 있음 ^^.
- Dropout (드랍아웃)
과적합을 해결할 수 있는 가장 간단한 방법으로는 Dropout이 있음. Dropout은 단어에서도 의미를 유추할 수 있듯이 각 노드들이 이어진 선을 빼서 없애버린다는 의미가 있음.

위 그림의 오른쪽 그림처럼 각 노드의 연결을 끊어버리는 작업을 하는데, 각 배치마다 랜덤한 노드를 끊어버림. 즉 다음 노드로 전달할 때 랜덤하게 출력을 0으로 만들어버리는 것과 같음.
"사공이 많으면 배가 산으로 간다"라는 속담처럼 과적합이 발생했을 때 적당한 노드들을 탈락시켜서 더 좋은 효과를 낼 수 있음.

위와 같이 전문가들이 너무 많다고 가정합시다. 귀만 판단하는 전문가, 꼬리만 판단하는 전문가 등등 너무 많은 전문가(노드)들이 있다면, 이들 중 일부만 사용해도 충분히 결과를 낼 수 있음. 오히려 이들 중에서 충분할 만큼의 전문가만 선출해서 반복적으로 결과를 낸다면, 오히려 균형 잡힌 훌륭한 결과가 나올 가능성이 높음.
Dropout은 과적합 발생시 생각보다 좋은 효과를 냅니다. (그리고 사용하기도 정말 간단) 실무에서 과적합이 발생한다면 꼭 한 번 사용해보자.
- Ensemble (앙상블)
앙상블 기법은 컴퓨팅 파워만 충분하다면 가장 시도해보기 쉬운 방법. 여러개의 딥러닝 모델을 만들어 각각 학습시킨 후 각각의 모델에서 나온 출력을 기반으로 투표를 하는 방법이죠. 앞에서 설명했던 랜덤 포레스트의 기법과 비슷.

앙상블 또한 개념적으로 이해하는 것이 중요한데 여러개의 모델에서 나온 출력에서 다수결로 투표(Majority voting)를 하는 방법도 있고, 평균값을 구하는 방법도 있고, 마지막에 결정하는 레이어를 붙이는 경우 등 다양한 방법으로 응용이 가능.
앙상블을 사용할 경우 최소 2% 이상의 성능 향상 효과를 볼 수 있다고 알려져 있음.
- Learning rate decay (Learning rate schedules)
Learning rate decay 기법은 실무에서도 자주 쓰는 기법으로 Local minimum에 빠르게 도달하고 싶을 때 사용.

위 사진에서보면 왼쪽 그림은 학습의 앞부분에서는 큰 폭으로 건너뛰고 뒷부분으로 갈 수록 점점 조금씩 움직여서 효율적으로 Local minimum을 찾는 모습임. 오른쪽 그림은 Learning rate를 고정시켰을 때의 모습.
또한 Learning rate decay 기법을 사용하면 Local minimum을 효과적으로 찾도록 도와줌. 아래 그림을 보면 Learning rate가 줄어들때마다 Error 값이 한 번씩 큰 폭으로 떨어지는 현상을 보임. 이렇게 하면 Local minimum을 찾기 쉽다.

Keras에서는 tf.keras.callbacks.LearningRateScheduler() 와 tf.keras.callbacks.ReduceLROnPlateau() 를 사용하여 학습중 Learning rate를 조절함. https://keras.io/api/callbacks/learning_rate_scheduler/ https://keras.io/api/callbacks/reduce_lr_on_plateau
Keras documentation: ReduceLROnPlateau
ReduceLROnPlateau ReduceLROnPlateau class tf.keras.callbacks.ReduceLROnPlateau( monitor="val_loss", factor=0.1, patience=10, verbose=0, mode="auto", min_delta=0.0001, cooldown=0, min_lr=0, **kwargs ) Reduce learning rate when a metric has stopped improving
keras.io
[ XOR 실습 ]
- 딥러닝으로 XOR 문제 풀어보기
https://colab.research.google.com/drive/1FO2LlqP9nmuVyslfGuFtw_it9pRdgiGq?usp=sharing
3주차 실습 - 01. 딥러닝 XOR의 사본
Colaboratory notebook
colab.research.google.com
- 코드 설명
필요한 패키지 임포트하기
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam, SGD
XOR 데이터셋 만들기
x_data = np.array([[0, 0], [0, 1], [1, 0], [1, 1]], dtype=np.float32)
y_data = np.array([[0], [1], [1], [0]], dtype=np.float32)
이진논리회귀로 풀어보기
model = Sequential([
Dense(1, activation='sigmoid')
])
model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.1))
model.fit(x_data, y_data, epochs=1000, verbose=0)
<결과>
/usr/local/lib/python3.7/dist-packages/keras/optimizer_v2/gradient_descent.py:102: UserWarning: The `lr` argument is deprecated, use `learning_rate` instead.
super(SGD, self).__init__(name, **kwargs)
<keras.callbacks.History at 0x7ff36dce0dd0>
y_pred = model.predict(x_data)
print(y_pred)
<결과>
[[0.4992855 ]
[0.5001897 ]
[0.49958602]
[0.50049025]]
딥러닝(MLP)로 풀어보기
model = Sequential([
Dense(8, activation='relu'),
Dense(1, activation='sigmoid'),
])
model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.1))
model.fit(x_data, y_data, epochs=1000, verbose=0)
<결과>
/usr/local/lib/python3.7/dist-packages/keras/optimizer_v2/gradient_descent.py:102: UserWarning: The `lr` argument is deprecated, use `learning_rate` instead.
super(SGD, self).__init__(name, **kwargs)
<keras.callbacks.History at 0x7ff36c42f710>
y_pred = model.predict(x_data)
print(y_pred)
<결과>
[[0.06793827]
[0.9882194 ]
[0.98845565]
[0.00782332]]
Keras Functional API 써보기
우리는 지금까지 Keras의 Sequential 클래스를 사용하여 Sequential API를 사용했음. Sequential API는 순차적인 모델 설계에는 편리한 API 이지만, 복잡한 네트워크를 설계하기에는 한계가 있기 때문에 실무에서는 Functional API를 주로 사용함.
위에서 했던 XOR 딥러닝 문제를 Functional API로 다시 작성해봄.!
import numpy as np
from tensorflow.keras.models import Sequential, Model
from tensorflow.keras.layers import Dense, Input
from tensorflow.keras.optimizers import Adam, SGDinput = Input(shape=(2,))
hidden = Dense(8, activation='relu')(input)
output = Dense(1, activation='sigmoid')(hidden)
model = Model(inputs=input, outputs=output)
model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.1))
model.summary()
<결과>
Model: "model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 2)] 0
dense_3 (Dense) (None, 8) 24
dense_4 (Dense) (None, 1) 9
=================================================================
Total params: 33
Trainable params: 33
Non-trainable params: 0
_________________________________________________________________
/usr/local/lib/python3.7/dist-packages/keras/optimizer_v2/gradient_descent.py:102: UserWarning: The `lr` argument is deprecated, use `learning_rate` instead.
super(SGD, self).__init__(name, **kwargs)model.summary() 를 사용하여 모델의 구조를 확인할 수 있음.
Sequential API를 사용하면 구조를 확인하기 힘들지만 Functional API를 사용하면 model.summary()를 사용하여 구조를 확인하기 쉽다는 장점도 있음.
model.fit(x_data, y_data, epochs=1000, verbose=0)
y_pred = model.predict(x_data)
<결과>
[[0.0811488 ]
[0.98076177]
[0.9900486 ]
[0.01074305]]
[ 딥러닝 실습 ]
- Sign Language MNIST (수화 알파벳) 실습
https://colab.research.google.com/drive/1VhnvBrKQFEyOZGS0IR5FegGWajqNsMZb?usp=sharing
3주차 실습 - 02. Sign Language MNIST
Colaboratory notebook
colab.research.google.com
- 코드 설명
[런타임Runtime] - [런타임 유형 변경Change runtime type] - GPU 선택해서 연산속도 늘리기
https://www.kaggle.com/datamunge/sign-language-mnist
Sign Language MNIST
Drop-In Replacement for MNIST for Hand Gesture Recognition Tasks
www.kaggle.com
데이터셋 다운로드
import os
os.environ['KAGGLE_USERNAME'] = 'username' # username
os.environ['KAGGLE_KEY'] = 'key' # key!kaggle datasets download -d datamunge/sign-language-mnist
<결과>
Downloading sign-language-mnist.zip to /content
66% 41.0M/62.6M [00:02<00:01, 18.7MB/s]
100% 62.6M/62.6M [00:02<00:00, 24.5MB/s]
!unzip sign-language-mnist.zip
<결과>
Archive: sign-language-mnist.zip
inflating: amer_sign2.png
inflating: amer_sign3.png
inflating: american_sign_language.PNG
inflating: sign_mnist_test.csv
inflating: sign_mnist_test/sign_mnist_test.csv
inflating: sign_mnist_train.csv
inflating: sign_mnist_train/sign_mnist_train.csv
필요한 패키지 임포트하기
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input, Dense
from tensorflow.keras.optimizers import Adam, SGD
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import OneHotEncoder
데이터셋 로드하기
train_df = pd.read_csv('sign_mnist_train.csv')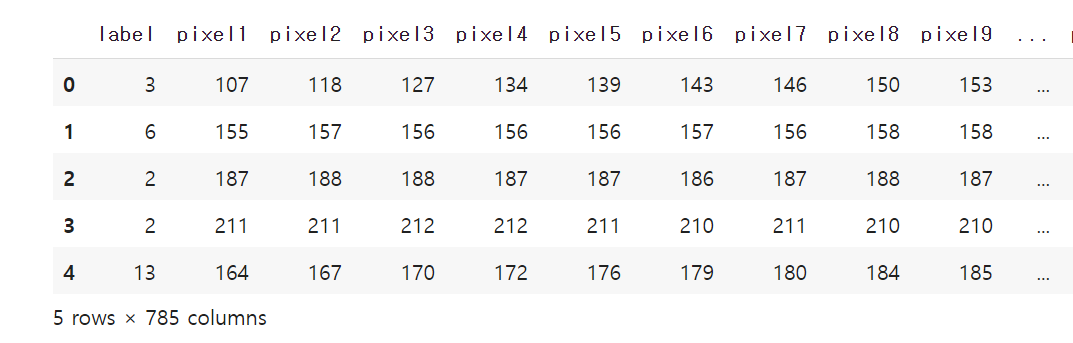
test_df = pd.read_csv('sign_mnist_test.csv')
라벨 분포 확인하기
plt.figure(figsize=(16, 10))
sns.countplot(train_df['label'])
plt.show()
전처리하기
전처리하기 - 입력과 출력 나누기
train_df = train_df.astype(np.float32)
x_train = train_df.drop(columns=['label'], axis=1).values
y_train = train_df[['label']].values
test_df = test_df.astype(np.float32)
x_test = test_df.drop(columns=['label'], axis=1).values
y_test = test_df[['label']].values
<결과>
(27455, 784) (27455, 1)
(7172, 784) (7172, 1)
전처리하기 - 데이터 미리보기
train_df = train_df.astype(np.float32)
x_train = train_df.drop(columns=['label'], axis=1).values
y_train = train_df[['label']].values
test_df = test_df.astype(np.float32)
x_test = test_df.drop(columns=['label'], axis=1).values
y_test = test_df[['label']].values
전처리하기 - one-hot 인코딩하기
encoder = OneHotEncoder()
y_train = encoder.fit_transform(y_train).toarray()
y_test = encoder.fit_transform(y_test).toarray()
<결과>
(27455, 24)
전처리하기 - 일반화하기
이미지 데이터는 픽셀이 0-255 사이의 정수(unsigned integer 8bit = uint8)로 되어 있음. 이것을 255로 나누어 0-1 사이의 소수점 데이터(floating point 32bit = float32)로 바꾸고 일반화 시키도록 함.
x_train = x_train / 255.
x_test = x_test / 255.
네트워크 구성하기
input = Input(shape=(784,))
hidden = Dense(1024, activation='relu')(input)
hidden = Dense(512, activation='relu')(hidden)
hidden = Dense(256, activation='relu')(hidden)
output = Dense(24, activation='softmax')(hidden)
model = Model(inputs=input, outputs=output)
model.compile(loss='categorical_crossentropy', optimizer=Adam(lr=0.001), metrics=['acc'])
model.summary()
<결과>
Model: "model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 784)] 0
dense (Dense) (None, 1024) 803840
dense_1 (Dense) (None, 512) 524800
dense_2 (Dense) (None, 256) 131328
dense_3 (Dense) (None, 24) 6168
=================================================================
Total params: 1,466,136
Trainable params: 1,466,136
Non-trainable params: 0
_________________________________________________________________
/usr/local/lib/python3.7/dist-packages/keras/optimizer_v2/adam.py:105: UserWarning: The `lr` argument is deprecated, use `learning_rate` instead.
super(Adam, self).__init__(name, **kwargs)
모델 학습시키기
history = model.fit(
x_train,
y_train,
validation_data=(x_test, y_test), # 검증 데이터를 넣어주면 한 epoch이 끝날때마다 자동으로 검증
epochs=20 # epochs 복수형으로 쓰기!
)
<결과>
Epoch 1/20
858/858 [==============================] - 7s 6ms/step - loss: 1.6571 - acc: 0.4610 - val_loss: 1.1096 - val_acc: 0.6269
Epoch 2/20
858/858 [==============================] - 5s 6ms/step - loss: 0.5916 - acc: 0.7930 - val_loss: 0.9230 - val_acc: 0.7168
Epoch 3/20
858/858 [==============================] - 5s 6ms/step - loss: 0.2669 - acc: 0.9074 - val_loss: 1.0416 - val_acc: 0.7549
Epoch 4/20
858/858 [==============================] - 5s 5ms/step - loss: 0.1886 - acc: 0.9391 - val_loss: 0.8058 - val_acc: 0.7910
Epoch 5/20
858/858 [==============================] - 5s 5ms/step - loss: 0.1229 - acc: 0.9586 - val_loss: 1.3429 - val_acc: 0.6701
Epoch 6/20
858/858 [==============================] - 5s 6ms/step - loss: 0.0883 - acc: 0.9725 - val_loss: 0.9020 - val_acc: 0.8264
Epoch 7/20
858/858 [==============================] - 5s 6ms/step - loss: 0.1201 - acc: 0.9623 - val_loss: 0.8704 - val_acc: 0.8259
Epoch 8/20
858/858 [==============================] - 5s 6ms/step - loss: 0.0415 - acc: 0.9874 - val_loss: 0.9210 - val_acc: 0.8339
Epoch 9/20
858/858 [==============================] - 5s 6ms/step - loss: 0.0883 - acc: 0.9738 - val_loss: 0.8724 - val_acc: 0.8261
Epoch 10/20
858/858 [==============================] - 5s 6ms/step - loss: 0.1017 - acc: 0.9665 - val_loss: 1.0212 - val_acc: 0.7812
Epoch 11/20
858/858 [==============================] - 5s 6ms/step - loss: 0.0363 - acc: 0.9888 - val_loss: 0.8614 - val_acc: 0.8430
Epoch 12/20
858/858 [==============================] - 5s 6ms/step - loss: 4.1568e-04 - acc: 1.0000 - val_loss: 0.9152 - val_acc: 0.8465
Epoch 13/20
858/858 [==============================] - 5s 6ms/step - loss: 2.0703e-04 - acc: 1.0000 - val_loss: 0.9763 - val_acc: 0.8458
Epoch 14/20
858/858 [==============================] - 5s 6ms/step - loss: 1.4430e-04 - acc: 1.0000 - val_loss: 1.0271 - val_acc: 0.8381
Epoch 15/20
858/858 [==============================] - 5s 6ms/step - loss: 8.2328e-05 - acc: 1.0000 - val_loss: 1.0913 - val_acc: 0.8351
Epoch 16/20
858/858 [==============================] - 5s 6ms/step - loss: 0.0713 - acc: 0.9933 - val_loss: 4.2734 - val_acc: 0.3540
Epoch 17/20
858/858 [==============================] - 5s 6ms/step - loss: 0.1698 - acc: 0.9461 - val_loss: 0.9186 - val_acc: 0.8231
Epoch 18/20
858/858 [==============================] - 5s 6ms/step - loss: 0.0017 - acc: 1.0000 - val_loss: 0.9984 - val_acc: 0.8165
Epoch 19/20
858/858 [==============================] - 5s 6ms/step - loss: 7.9769e-04 - acc: 1.0000 - val_loss: 1.1602 - val_acc: 0.8111
Epoch 20/20
858/858 [==============================] - 5s 6ms/step - loss: 0.1449 - acc: 0.9540 - val_loss: 0.9128 - val_acc: 0.8272
학습 결과 보기
plt.figure(figsize=(16, 10))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
정확도 보기
plt.figure(figsize=(16, 10))
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
[ 과제 실습 - 숫자 MNIST ]
- 과제 내용
[ 데이터 셋 다운로드 ]
- kaggle 로그인 정보 입력
import os
os.environ['KAGGLE_USERNAME'] = 'XXX' # username
os.environ['KAGGLE_KEY'] = 'XXX-Key' # key
- 압축 (데이터셋)파일 가져오기
!kaggle datasets download -d oddrationale/mnist-in-csv
<결과>
Downloading mnist-in-csv.zip to /content
0% 0.00/15.2M [00:00<?, ?B/s]
100% 15.2M/15.2M [00:00<00:00, 183MB/s]
- 압축 해제
!unzip mnist-in-csv.zip
<결과>
Archive: mnist-in-csv.zip
inflating: mnist_test.csv
inflating: mnist_train.csv
[ Python Package 로드 ]
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input, Dense
from tensorflow.keras.optimizers import Adam, SGD
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import OneHotEncoder
[ 데이터셋 메모리 로드 - 트레이닝 데이터셋 ]
train_df = pd.read_csv('mnist_train.csv')
train_df.head()
<결과>
label 1x1 1x2 1x3 1x4 1x5 1x6 1x7 1x8 1x9 ... 28x19 28x20 28x21 28x22 28x23 28x24 28x25 28x26 28x27 28x28
0 5 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
2 4 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
3 1 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
4 9 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
5 rows × 785 columns
[ 데이터셋 메모리 로드 - 테스트 데이터셋 ]
test_df = pd.read_csv('mnist_test.csv')
test_df.head()
<결과>
label 1x1 1x2 1x3 1x4 1x5 1x6 1x7 1x8 1x9 ... 28x19 28x20 28x21 28x22 28x23 28x24 28x25 28x26 28x27 28x28
0 7 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
1 2 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
2 1 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
3 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
4 4 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
5 rows × 785 columns
[ 라벨분포 확인 ]
plt.figure(figsize=(16, 10))
sns.countplot(train_df['label'])
plt.show()
[ 전처리 - 입력과 출력 나누기 ]
train_df = train_df.astype(np.float32)
x_train = train_df.drop(columns=['label'], axis=1).values
y_train = train_df[['label']].values
test_df = test_df.astype(np.float32)
x_test = test_df.drop(columns=['label'], axis=1).values
y_test = test_df[['label']].values
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)
<결과>
(60000, 784) (60000, 1)
(10000, 784) (10000, 1)
[ 데이터 미리보기 ]
index = 1
plt.title(str(y_train[index]))
plt.imshow(x_train[index].reshape((28, 28)), cmap='gray')
plt.show()
[ One-hot encoding ]
encoder = OneHotEncoder()
y_train = encoder.fit_transform(y_train).toarray()
y_test = encoder.fit_transform(y_test).toarray()
print(y_train.shape)
<결과>
(60000, 10)
[ 일반화 ]
x_train = x_train / 255.
x_test = x_test / 255.
[ 네트워크 구성 ]
input = Input(shape=(784,))
hidden = Dense(1024, activation='relu')(input)
hidden = Dense(512, activation='relu')(hidden)
hidden = Dense(256, activation='relu')(hidden)
output = Dense(10, activation='softmax')(hidden)
model = Model(inputs=input, outputs=output)
model.compile(loss='categorical_crossentropy', optimizer=Adam(lr=0.001), metrics=['acc'])
model.summary()
<결과>
Model: "model_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_2 (InputLayer) [(None, 784)] 0
dense_4 (Dense) (None, 1024) 803840
dense_5 (Dense) (None, 512) 524800
dense_6 (Dense) (None, 256) 131328
dense_7 (Dense) (None, 10) 2570
=================================================================
Total params: 1,462,538
Trainable params: 1,462,538
Non-trainable params: 0
_________________________________________________________________
/usr/local/lib/python3.7/dist-packages/keras/optimizer_v2/adam.py:105: UserWarning: The `lr` argument is deprecated, use `learning_rate` instead.
super(Adam, self).__init__(name, **kwargs)
[ 학습 ]
history = model.fit(
x_train,
y_train,
validation_data=(x_test, y_test), # 검증 데이터를 넣어주면 한 epoch이 끝날때마다 자동으로 검증
epochs=20 # epochs 복수형으로 쓰기!
)
<결과>
Epoch 1/20
1875/1875 [==============================] - 14s 6ms/step - loss: 0.1935 - acc: 0.9409 - val_loss: 0.1114 - val_acc: 0.9654
Epoch 2/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0902 - acc: 0.9727 - val_loss: 0.0833 - val_acc: 0.9759
Epoch 3/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0649 - acc: 0.9800 - val_loss: 0.0772 - val_acc: 0.9769
Epoch 4/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0506 - acc: 0.9845 - val_loss: 0.1150 - val_acc: 0.9676
Epoch 5/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0400 - acc: 0.9878 - val_loss: 0.0849 - val_acc: 0.9794
Epoch 6/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0367 - acc: 0.9886 - val_loss: 0.0651 - val_acc: 0.9830
Epoch 7/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0300 - acc: 0.9911 - val_loss: 0.0866 - val_acc: 0.9761
Epoch 8/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0274 - acc: 0.9918 - val_loss: 0.0855 - val_acc: 0.9817
Epoch 9/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0258 - acc: 0.9927 - val_loss: 0.0867 - val_acc: 0.9799
Epoch 10/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0232 - acc: 0.9931 - val_loss: 0.0948 - val_acc: 0.9787
Epoch 11/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0222 - acc: 0.9938 - val_loss: 0.1051 - val_acc: 0.9817
Epoch 12/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0213 - acc: 0.9940 - val_loss: 0.1158 - val_acc: 0.9789
Epoch 13/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0187 - acc: 0.9950 - val_loss: 0.1134 - val_acc: 0.9783
Epoch 14/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0196 - acc: 0.9948 - val_loss: 0.1110 - val_acc: 0.9814
Epoch 15/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0182 - acc: 0.9954 - val_loss: 0.1004 - val_acc: 0.9817
Epoch 16/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0171 - acc: 0.9963 - val_loss: 0.1156 - val_acc: 0.9831
Epoch 17/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0169 - acc: 0.9959 - val_loss: 0.1338 - val_acc: 0.9829
Epoch 18/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0197 - acc: 0.9954 - val_loss: 0.1043 - val_acc: 0.9816
Epoch 19/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0156 - acc: 0.9966 - val_loss: 0.1827 - val_acc: 0.9766
Epoch 20/20
1875/1875 [==============================] - 10s 5ms/step - loss: 0.0165 - acc: 0.9963 - val_loss: 0.1369 - val_acc: 0.9829
[ 학습 결과 그래프 확인하기 ]
plt.figure(figsize=(16, 10))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
[ 학습 정확도 확인하기 ]
plt.figure(figsize=(16, 10))
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
[ 최종 결과 colab 링크 ]
https://colab.research.google.com/drive/1FZTgrzEuw6W8nQJGEf3uFFCpCQ_M68tj?usp=sharing
'ICT 학습' 카테고리의 다른 글
| 웹개발 종합반 - 3주차 (0) | 2022.04.29 |
|---|---|
| 이미지 처리로 시작하는 딥러닝 - 3주차 (0) | 2022.04.26 |
| 웹개발 종합반 - 2주차 (0) | 2022.04.25 |
| 이미지 처리로 시작하는 딥러닝 - 2주차 (0) | 2022.04.24 |
| 머신러닝 기본부터 다시 배우기 - 2주차 (0) | 2022.04.23 |



